非線形制御

非線形制御（ひせんけいせいぎょ、英: Nonlinear control）は、制御工学において、とりわけ非線形または時変（英語版）のシステム、あるいは両者を扱う制御方式。

多くの確立した解析および設計技術が、線形時不変系（LTIシステム）に存在する。 （例えば根軌跡（英語版）、ボード線図、ナイキスト安定判別法（英語版）、状態フィードバック、極配置（英語版）。） しかしながら、一般的な制御システムにある制御器と制御対象の一方あるいは両方は、LTIシステムでない可能性がある。したがって、これらの方法は必ずしも直接適用することができない。

非線形制御理論は、これらの一般的な制御システムに、既存の線形システムでの手法をどのように適用するかを研究する。

さらに、非線形制御理論は、LTIシステム理論を使用して解析することができない新しい制御方法を提供する。

LTIシステム理論を制御器の解析と設計に使用することができる場合であっても、非線形制御器が魅力的な特性となることがある（例えば、より単純な実装、より高速な動作、より少ない制御電力といった特性）。

非線形制御理論を証明するためには、厳密な解析学が必要となることが多い。

非線形システムの特性

非線形動的システムの特性は以下の通り。

• 重ね合わせの原理（線形性と均質）に従わない。
• 多数の分離された均衡点が存在する可能性がある。
• リミットサイクル、分岐、カオスのような特性を示す場合がある。
• 有限の逃避時間 (escape time): 非線形システムの解が常に存在するとは限らない。

非線形システムの解析と制御

十分に発達したいくつかの非線形フィードバックシステムの解析手法がある:

• 記述関数（英語版）法^[1][2]
• 位相面法（英語版）^[1]
• リアプノフ安定解析
• 特異摂動（英語版）法^[3]
• ポポフ（Popov）（英語版）条件^[4]（後述のLur'e問題を参照）
• 中心多様体理論（英語版）
• 小利得の定理（英語版）
• 受動性解析（英語版）

非線形システムのための制御設計技術も存在する。 この方法は、特定の限られた範囲を線形システムとして扱うことを試みる技術と細分化することができる:

• ゲイン・スケジューリング（英語版）

システムを線形として扱い制御設計を行えるように、補助的な非線形フィードバックを導入することを試みる方法:

• フィードバック線形化（英語版）

リャプノフに基づいた方法:

• リャプノフの再設計法（英語版）
• 非線形減衰（英語版）
• Backstepping
• スライディングモード制御（英語版）

非線形フィードバック解析とルーリエ問題

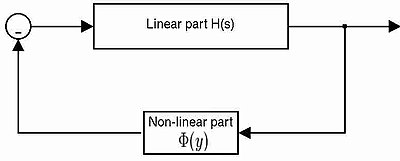
初期の非線形フィードバックシステム解析問題はアナトリー・イサコビッチ・ルーリエによって公式化された。 ルーリエ問題で取り扱われている制御システムは、線形で時間不変のフォワード経路と、メモリのない時変で静的非線形のフィードバック経路を有する。

線形部は4つの行列 (A,B,C,D) で表すことができ、一方、非線形部は次式で示すΦ(y)で表すことができる。

${\displaystyle {\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y}$ (セクタ非線形)

絶対安定問題

次の条件について検討する:

1. (A,B) は制御可能で、(C,A) は観測可能
2. 関数Φのセクターを定義するための2つの実数 a,b について a<b

x=0がシステム全体で一様に漸近安定の平衡であるといった、伝達行列 H(s) および {a,b} のみを含む条件を引き出すことが問題である。 これはルーリエ問題として知られている。

2つの主要な定理がこの問題に関係する:

• 円盤条件（英語版）^[4]
• ポポフ（英語版）条件^[4]

これらは、絶対安定の十分条件を与える。

ポポフ条件

ポポフ（Popov）（英語版）によって研究されたルーリエシステムのサブクラスは次式によって表される:

${\displaystyle {\begin{matrix}{\dot {x}}&=&Ax+bu\\{\dot {\xi }}&=&u\\y&=&cx+d\xi \quad (1)\end{matrix}}}$

${\displaystyle {\begin{matrix}u=-\phi (y)\quad (2)\end{matrix}}}$

ここで x ∈ Rⁿ であり、 ξ,u,y はスカラー量、 A,b,c,d は同一の次元である。 Φ: R → R は、開セクタ（open sector） (0, ∞) に属する時不変な非線形要素である。 これは、次式であることを意味する。

Φ(0) = 0, y Φ(y) > 0, ∀ y ≠ 0;

uからyまでの伝達関数は次式で与えられる。

${\displaystyle H(s)={\frac {d}{s}}+c(sI-A)^{-1}b\quad \quad }$

定理: 上記 (1)-(2) のシステムにおいて、次の条件を仮定する。

1. A はフルビッツ行列
2. (A,b) は制御可能
3. (A,c) は観測可能
4. d > 0
5. Φ ∈ (0,∞)

次式に示すような値 r>0 が存在する場合、システムは全体的に漸近安定であると言える。

inf_{ω ∈ R} Re[(1+jωr)h(jω)] > 0

補足

• ポポフ条件は自律システムにのみ適用可能である。
• ポポフによって研究されたシステムは、原点で極を持っており、入力から出力まで直接の経路がない。
• 非線形Φは開セクター条件を満たさなければならない。

非線形制御での理論

フロベニウスの定理

フロベニウスの定理（英語版）は微分幾何学中の深い結果（deep result）（英語版）である。 非線形制御に適用した場合、次のことが言える:

『${\displaystyle x\in R^{n}}$, ${\displaystyle f_{1},\dots ,f_{k}}$ が分散 ${\displaystyle \Delta }$ に属するベクトル場であり、${\displaystyle u_{i}(t)}$ が制御関数であるとき、式

${\displaystyle {\dot {x}}=\sum _{i=1}^{k}f_{i}(x)u_{i}(t)\,}$

で与えられたシステムにおいて、 スパン(${\displaystyle \Delta =m}$) と${\displaystyle \Delta }$が対合（involutive）な分散ならば、 ${\displaystyle x}$の積分曲線が次元${\displaystyle m}$ の多様体に制限される』

関連項目

• 帰還不働化（英語版）^[5]
• 位相同期回路（PLL）

参考文献

関連文献