Barisan eksak

Barisan eksak adalah sebuah konsep dalam matematika, khususnya dalam teori grup, gelanggang dan modul teori, aljabar homologis, serta dalam geometri diferensial. Barisan eksak adalah barisan terbatas atau tak terbatas dari objek dan morfisme sedemikian sehingga peta dari satu morfisme sama dengan kernel yang berikutnya.

Definisi

Dalam konteks teori grup, sebuah barisan

dari grup dan homomorfisme grup disebut eksak jika peta dari setiap homomorfisme sama dengan kernel dari homomorfisme berikutnya:untuk setiap ${\displaystyle k}$. Di sini, barisan grup beserta homomorfismenya dapat bersifat terbatas, maupun tidak terbatas.

Definisi serupa dapat dibuat untuk struktur aljabar lainnya. Misalnya barisan dari ruang vektor dan transformasi linear, atau dari modul dan homomorfisme modul. Secara umum, konsep barisan eksak dapat didefinisikan pada kategori yang memiliki kernel dan kokernel.

Kasus sederhana

Untuk memahami pengertian dari barisan eksak, mari meninjau kasus-kasus sederhana dengan barisan bersifat terbatas yang dimulai atau diakhiri dengan grup trivial. Biasanya, grup trivial dengan elemen identitas tunggal, dilambangkan dengan 0 (notasi aditif, biasanya jika grupnya abelian), atau dilambangkan 1 (notasi perkalian).

• Tinjau barisan ${\displaystyle 0\rightarrow A\rightarrow B}$. Peta pemetaan paling kiri adalah ${\displaystyle 0}$. Oleh karena itu, barisan ini eksak jika dan hanya jika pemetaan paling kanan (dari ${\displaystyle A}$ ke ${\displaystyle B}$) memiliki kernel ${\displaystyle 0}$; yaitu jika dan hanya jika pemetaan paling kanan adalah monomorfisme (injektif, atau satu-ke-satu).
• Tinjau barisan ${\displaystyle B\rightarrow C\rightarrow 0}$. Kernel peta paling kanan adalah ${\displaystyle C}$. Oleh karena itu, barisan ini eksak jika dan hanya jika peta pemetaan paling kiri (dari ${\displaystyle B}$ ke ${\displaystyle C}$) adalah ${\displaystyle C}$; yaitu jika dan hanya jika pemetaan paling kanan adalah epimorfisme (perkiraan, atau ke atas).
• Oleh karena itu, barisan ${\displaystyle 0\rightarrow X\rightarrow Y\rightarrow 0}$ eksak jika dan hanya jika pemetaan dari ${\displaystyle X\rightarrow Y}$ adalah monomorfisme dan epimorfisme (yaitu, bimorfisme), yang biasanya juga merupakan isomorfisme antara ${\displaystyle X}$ dan ${\displaystyle Y}$ (hal ini berlaku pada kategori eksak seperti kategori himpunan).

Barisan eksak pendek

Barisan eksak pendek merupakan barisan eksak berbentuk

.

Dari pembahasan di atas, barisan di atas merupakan barisan eksak pendek jika dan hanya jika ${\displaystyle f}$ adalah monomorfisme, ${\displaystyle g}$ adalah epimorfisme, dan peta dari ${\displaystyle f}$ sama dengan kernel ${\displaystyle g}$. Untuk memudahkan, pandang ${\displaystyle A}$ sebagai subobjek dari ${\displaystyle B}$ dengan ${\displaystyle f}$ pemetaan yang "memasukkan" ${\displaystyle A}$ ke dalam ${\displaystyle B}$, dan ${\displaystyle C}$ sebagai objek faktor (atau hasil bagi) ${\displaystyle B/A}$ melalui isomorfisme yang diinduksi oleh ${\displaystyle g}$ berikut.

.

Barisan eksak pendek

disebut 'split' jika terdapat homomorfisme ${\displaystyle h:C\rightarrow B}$ sedemikian sehingga ${\displaystyle g\circ h=\mathrm {id} _{C}}$, dengan ${\displaystyle \mathrm {id} _{C}}$ adalah pemetaan identitas pada ${\displaystyle C}$Akibatnya, jika barisan ini merupakan barisan eksak dari grup abelian, ${\displaystyle B}$ isomorfik terhadap jumlah langsung dari ${\displaystyle A}$ dan ${\displaystyle C}$:${\displaystyle B\cong A\oplus C.}$

Barisan eksak panjang

Barisan eksak panjang adalah barisan eksak yang terdiri dari lebih dari tiga suku bukan nol, sering kali merupakan barisan eksak tak terbatas.

Barisan eksak panjang ekuivalen dengan kumpulan barisan eksak pendek. Misalkan

adalah barisan eksak panjang dengan ${\displaystyle n\geq 2}$, maka barisan eksak ini dapat dipecah menjadi beberapa barisan eksak pendek

dimana ${\displaystyle K_{i}=\operatorname {im} (f_{i})=\ker(f_{i+1})}$ untuk ${\displaystyle i}$.

Contoh

Bilangan bulat modulo dua

Tinjau barisan eksak grup abelian berikut:

Homomorfisme pertama memetakan setiap ${\displaystyle i\in \mathbb {Z} }$ ke ${\displaystyle 2i\in \mathbb {Z} }$. Homomorfisme kedua memetakan setiap ${\displaystyle i\in \mathbb {Z} }$ ke ${\displaystyle i{\bmod {2}}}$. Di sini panah kait ${\displaystyle \hookrightarrow }$ menunjukkan bahwa pemetaan ${\displaystyle 2\times }$ dari ${\displaystyle \mathbb {Z} }$ ke ${\displaystyle \mathbb {Z} }$ adalah monomorfisme, dan panah berkepala dua ${\displaystyle \twoheadrightarrow }$ menunjukkan epimorfisme (pemetaan modulo 2). Ini adalah barisan eksak, karena peta dari monomorfisme ${\displaystyle 2\times }$ adalah kernel dari epimorfisme. Pada dasarnya, barisan yang "sama" juga dapat ditulis sebagai

Dalam hal ini, monomorfismenya adalah pemetaan inklusi ${\displaystyle 2n\mapsto 2n}$, yang meskipun terlihat seperti fungsi identitas, bukanlah fungsi identitas (bukan epimorfisme), karena bilangan ganjil bukanlah elemen ${\displaystyle 2\mathbb {Z} }$. Peta dari ${\displaystyle \mathbb {2Z} }$ melalui monomorfisme ini adalah subhimpunan dari ${\displaystyle \mathbb {Z} }$ yang merupakan peta dari pemetaan ${\displaystyle n\mapsto 2n}$ yang digunakan dalam barisan eksak sebelumnya. Secara konkret, barisan eksak ini berbeda dengan barisan eksak sebelumnya, mengingat objek pertama barisan eksak ini adalah ${\displaystyle 2\mathbb {Z} }$ dan objek pertama pada barisan sebelumnya adalah ${\displaystyle \mathbb {Z} }$, meskipun keduanya isomorfik sebagai grup.

Barisan eksak pada contoh pertama juga dapat ditulis tanpa menggunakan simbol khusus untuk monomorfisme dan epimorfisme:

Di sini ${\displaystyle 0}$ menunjukkan grup trivial, pemetaan dari ${\displaystyle \mathbb {Z} }$ ke ${\displaystyle \mathbb {Z} }$ adalah perkalian dengan ${\displaystyle 2}$, dan pemetaan dari ${\displaystyle \mathbb {Z} }$ ke grup faktor ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$ adalah pemetaan modulo ${\displaystyle 2}$. adalah barisan yang eksak, mengingat:

• peta pemetaan ${\displaystyle 0\rightarrow \mathbb {Z} }$ adalah ${\displaystyle 0}$, dan kernel dari perkalian dengan ${\displaystyle 2}$ juga adalah ${\displaystyle 0}$, sehingga barisannya eksak di ${\displaystyle \mathbb {Z} }$ pertama.
• peta perkalian dengan ${\displaystyle 2}$ adalah ${\displaystyle 2\mathbb {Z} }$, dan kernel dari pemetaan modulo ${\displaystyle 2}$ juga adalah ${\displaystyle 2\mathbb {Z} }$, sehingga barisannya eksak di ${\displaystyle \mathbb {Z} }$ kedua.
• peta pemetaan modulo 2 adalah ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$, dan kernel dari pemetaan nol juga adalah ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$, sehingga barisannya eksak di ${\displaystyle \mathbb {Z} /\mathbb {2Z} }$.

Perhatikan kembali barisan eksak pertama dan ketiga. Pada kedua barisan tersebut, pemetaan inklusi dari ${\displaystyle \mathbb {Z} }$ ke ${\displaystyle \mathbb {Z} }$ merupakan endomorfisme dari ${\displaystyle \mathbb {Z} }$ yang merupakan monomorfisme. Hal ini memungkinkan untuk ${\displaystyle \mathbb {Z} }$, karena ${\displaystyle \mathbb {Z} }$ adalah grup tak hingga. Tidak seperti ${\displaystyle \mathbb {Z} }$, grup berhingga tidak mungkin dipetakan oleh pemetaan inklusi (oleh monomorfisme) sebagai subgrup sejati dari grup berhingga itu sendiri. Sebaliknya, secara umum, barisan eksak pendek grup berhingga, berdasarkan teorema isomorfisme pertama, dapat ditulis sebagai berikut

Berikut contoh yang lebih konkret dari barisan eksak grup berhingga:

dengan ${\displaystyle C_{n}}$ adalah grup siklik dari order n dan ${\displaystyle D_{2n}}$ adalah grup dihedral dari order 2n, yang merupakan grup nonabelian.

Irisan dan jumlah modul

Misalkan I dan J adalah dua ideal dari sebuah gelanggang R. Maka

adalah barisan yang eksak modul-R, dengan homomorfisme modul ${\displaystyle I\cap J\to I\oplus J}$ memetakan setiap elemen ${\displaystyle x\in I\cap J}$ ke elemen ${\displaystyle (x,x)}$ pada jumlah langsung ${\displaystyle I\oplus J}$, dan homomorfisme ${\displaystyle I\oplus J\to I+J}$ memetakan setiap elemen ${\displaystyle (x,y)}$ dari ${\displaystyle I\oplus J}$ ke ${\displaystyle x-y}$.

Homomorfisme-homomorfisme pada barisan eksak di atas dapat dilihat sebagai batasan dari homomorfisme-homomorfisme yang didefinisikan secara serupa pada barisan eksak pendek berikut

Dengan menggunakan modul hasil bagi, barisan eksak ini menghasilkan barisan eksak yang sama persis dengan barisan eksak di atas

Sifat barisan eksak

Lema split menyatakan barisan eksak pendek

merupakan barisan eksak yang 'split', i.e. ${\displaystyle B\cong A\oplus C}$ , jika dan hanya jika terdapat morfisme ${\displaystyle t:B\rightarrow A}$ sedemikian sehingga ${\displaystyle t\circ f=\operatorname {id} _{A}}$ atau terdapat morfisme ${\displaystyle u:C\rightarrow B}$ sedemikian sehingga ${\displaystyle g\circ u=\operatorname {id} _{C}}$.

Lema ular memperlihatkan bahwa diagram komutatif dengan dua baris eksak menginduksi barisan eksak panjang. Lema sembilan adalah contoh khusus dari aplikasi lema ular.

Lema lima memberikan kondisi untuk pemetaan di tengah pada diagram komutatif dengan dua baris eksak memiliki panjang 5 menjadi isomorfisme; lema pendek lima merupakan contoh khusus dari aplikasi lema lima pada barisan eksak pendek.

Fakta bahwa setiap barisan eksak dapat dilihat sebagai hasil dari "menghubungkan" beberapa barisan eksak pendek yang tumpang tindih menunjukkan betapa pentingnya barisan eksak pendek. Sebagai contoh, tinjau barisan eksak berikut

yang mengimplikasikan terdapat objek ${\displaystyle C_{k}}$ pada kategori objek barisan tersebut sedemikian sehingga

Misalkan pula kokernel setiap morfisme pada barisan ada pada kategori objek barisan tersebut, dan isomorfis dengan peta morfisme setelahnya pada barisan eksak di atas:

(Ini benar untuk beberapa kategori, termasuk kategori abelian seperti kategori grup abelian, tetapi namun tidak benar untuk semua kategori yang mengenal konsep barisan eksak, dan khususnya tidak benar untuk kategori grup; spesifiknya ${\displaystyle \operatorname {coker} (f):G\rightarrow H}$ bukanlah ${\displaystyle H/\operatorname {Im} (f)}$, tetapi adalah grup hasil bagi ${\displaystyle H}$ dengan tutupan normal dari ${\displaystyle \operatorname {Im} (f)}$, i.e. irisan semua subgrup normal dari ${\displaystyle H}$ yang memuat ${\displaystyle \operatorname {Im} (f)}$.) Dengan demikian, kita mendapati diagram komutatif berikut yang setiap diagonalnya adalah barisan eksak pendek:

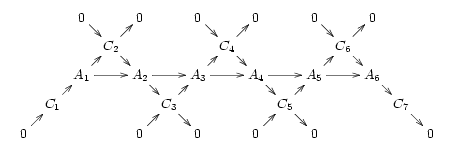
Bagian dari diagram ini yang bergantung pada eksistensi kokernel di kategori objek barisan adalah objek ${\displaystyle C_{7}}$ dan pasangan morfisme terakhir ${\displaystyle A_{6}\rightarrow C_{7}\rightarrow 0}$. Hal ini dikarenakan adanya objek ${\displaystyle A_{k+1}}$ dan morfisme ${\displaystyle A_{k}\rightarrow A_{k+1}}$ sedemikian sehingga ${\displaystyle A_{k-1}\rightarrow A_{k}\rightarrow A_{k+1}}$ adalah barisan yang eksak juga membuat barisan ${\displaystyle 0\rightarrow C_{k}\rightarrow A_{k}\rightarrow C_{k+1}\rightarrow 0}$ menjadi eksak. Dengan demikian, misalnya pada kategori grup, ${\displaystyle \operatorname {im} (f)}$ adalah kernel dari suatu homomorfisme dengan domain ${\displaystyle H}$ mengimplikasikan bahwa ${\displaystyle \operatorname {im} (f)}$ adalah subgrup normal dari ${\displaystyle H}$. Oleh karena itu, ${\displaystyle \operatorname {coker} (f)}$ isomorfik dengan hasil peta dari ${\displaystyle H/\operatorname {im} (f)}$ oleh pemetaan berikutnya.

Sebaliknya, jika diberikan sembarang kumpulan barisan eksak pendek yang saling tumpah tindih, maka suku tengah barisan eksak membentuk suatu barisan eksak dengan cara yang serupa.

Penerapan barisan eksak

Dalam teori kategori abelian, barisan eksak pendek seringkali digunakan sebagai media untuk membicarakan subobjek dan objek faktor.

Masalah ekstensi pada dasarnya adalah pertanyaan "Misalkan ${\displaystyle A}$ dan ${\displaystyle C}$ adalah suku akhir tidak nol pada barisan eksak pendek, apa yang dapat dikatakan mengenai suku tengah ${\displaystyle B}$ ?" Dalam kategori grup, ini ekuivalen dengan pertanyaan, "Grup ${\displaystyle B}$ apakah yang memiliki ${\displaystyle A}$ sebagai subgrup normalnya dengan ${\displaystyle C}$ merupakan grup hasil baginya?" Masalah ini penting dalam klasifikasi grup. Lihat pula grup automorfisme luar.

Perhatikan bahwa komposisi ${\displaystyle f_{i+1}\circ f_{i}}$ dalam barisan eksak merupakan pemetaan ${\displaystyle 0}$ dari ${\displaystyle A_{i}}$ ke ${\displaystyle A_{i+2}}$, sehingga setiap barisan eksak adalah rantai kompleks. Selanjutnya, hanya peta dari ${\displaystyle f_{i}}$ yang dipetakan ke ${\displaystyle 0}$ oleh ${\displaystyle f_{i+1}}$, sehingga homologi dari rantai kompleks (yaitu ${\displaystyle H_{i}=\ker(f_{i+1})/\mathrm {im} (f_{i})}$) semuanya trivial (merupakan grup nol). Dalam bahasa rantai kompleks, barisan eksak disebut rantai asiklik. Dari pembahasan sebelumnya, hal ini ekuivalen dengan rantai kompleks yang memiliki homologi trivial

Pada sembarang rantai kompleks, homologi dapat dianggap sebagai alat yang mengukur kegagalan rantai kompleks menjadi barisan yang eksak.

Jika barisan eksak pendek dihubungkan sedemikian rupa menjadi sebuah rantai kompleks (yaitu, barisan eksak pendek yang sukunya berupa rantai kompleks, atau dari sudut pandang lain, rantai kompleks yang sukunya berupa barisan eksak pendek), maka barisan eksak panjang dari homologi (yaitu barisan eksak yang tidak terbatas) dapat dikonstruksi dengan menggunakan lema zig-zag. Hal ini muncul di topologi aljabar dalam studi tentang homologi relatif; barisan Mayer–Vietoris adalah contoh lain. Praktik mengkonstruksi barisan eksak panjang dari barisan eksak pendek seperti ini juga muncul pada pembahasan funktor turunan.

Funktor yang mengirimkan barisan eksak ke barisan eksak disebut funktor eksak.

Daftar pustaka

• Spanier, Edwin Henry (1995). Algebraic Topology. Berlin: Springer. hlm. 179. ISBN 0-387-94426-5. 
• Eisenbud, David (1995). Commutative Algebra: with a View Toward Algebraic Geometry. Springer-Verlag New York. hlm. 785. ISBN 0-387-94269-6. 

Kutipan

Pranala luar

• Exact sequence, PlanetMath.org.