Curva del manjar blanco

En matemáticas, la curva del manjar blanco es un tipo de curva autoafín construible por subdivisiones sucesivas aplicadas en los puntos medios de cada estado anterior. También se conoce como la curva de Takagi, en honor a Teiji Takagi, quien la describió en 1901, o como la curva de Takagi-Landsberg, una generalización de la curva que lleva el nombre de Takagi y de Georg Landsberg.^[1]​ Su nombre proviene de su parecido con un manjar blanco,^[2]​ un tipo de pudding de origen francés. Es un caso particular de la curva de De Rham (véase curva fractal).

Definición

La función manjar blanco se define en el intervalo unidad mediante

${\displaystyle {\rm {blanc}}(x)=\sum _{n=0}^{\infty }{s(2^{n}x) \over 2^{n}},}$

donde ${\displaystyle s(x)}$ es una onda triangular, definida por ${\displaystyle s(x)=\min _{n\in {\mathbf {Z} }}|x-n|}$, es decir, ${\displaystyle s(x)}$ es la distancia de x al número entero más cercano.

La curva de Takagi-Landsberg es una ligera generalización, dada por

${\displaystyle T_{w}(x)=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)}$

para un parámetro ${\displaystyle w}$; por lo tanto, la curva del manjar blanco es el caso ${\displaystyle w=1/2}$. El valor ${\displaystyle H=-\log _{2}w}$ se conoce como parámetro de Hurst.

La función se puede extender a toda la recta real: la aplicación de la definición dada arriba muestra que la función se repite en cada intervalo unitario.

La función también podría estar definida por la serie en la sección Expansión en series de Fourier.

Definición de la ecuación funcional

La versión periódica de la curva de Takagi también se puede definir como la solución limitada única ${\displaystyle T=T_{w}:\mathbb {R} \to \mathbb {R} }$ a la ecuación funcional

${\displaystyle T(x)=s(x)+wT(2x)}$.

De hecho, la función del manjar blanco ${\displaystyle T_{w}}$ ciertamente está acotada y resuelve la ecuación funcional, ya que

${\displaystyle T_{w}(x):=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)=s(x)+\sum _{n=1}^{\infty }w^{n}s(2^{n}x)}$${\displaystyle =s(x)+w\sum _{n=0}^{\infty }w^{n}s(2^{n+1}x)=s(x)+wT_{w}(2x)}$.

Por el contrario, si ${\displaystyle T:\mathbb {R} \to \mathbb {R} }$ es una solución acotada de la ecuación funcional, iterando la igualdad que se tiene para cualquier N

${\displaystyle T(x)=\sum _{n=0}^{N}w^{n}s(2^{n}x)+w^{N+1}T(2^{N+1}x)=\sum _{n=0}^{N}w^{n}s(2^{n}x)+o(1)}$, para ${\displaystyle N\to \infty ,}$

de donde ${\displaystyle T=T_{w}}$. Por cierto, las ecuaciones funcionales anteriores poseen infinitas soluciones continuas, no acotadas, como por ejemplo ${\displaystyle T_{w}(x)+c|x|^{-\log _{2}w}.}$

Construcción gráfica

La curva del manjar blanco se puede construir visualmente a partir de funciones de onda triangulares si la suma infinita se aproxima mediante sumas finitas de los primeros términos. En las siguientes ilustraciones, las funciones triangulares progresivamente más finas (mostradas en rojo) se agregan a la curva en cada etapa.

n = 0	n ≤ 1	n ≤ 2	n ≤ 3

Propiedades

Convergencia y continuidad

La suma infinita que define ${\displaystyle T_{w}(x)}$ converge absolutamente para todo ${\displaystyle x}$: desde ${\displaystyle 0\leq s(x)\leq 1/2}$ para todo ${\displaystyle x\in \mathbb {R} }$, tiene:

${\displaystyle \sum _{n=0}^{\infty }|w^{n}s(2^{n}x)|\leq {\frac {1}{2}}\sum _{n=0}^{\infty }|w|^{n}={\frac {1}{2}}\cdot {\frac {1}{1-|w|}}}$ si ${\displaystyle |w|<1}$.

Por lo tanto, la curva de Takagi de parámetro ${\displaystyle w}$ se define en el intervalo unitario (o ${\displaystyle \mathbb {R} }$) si ${\displaystyle |w|<1}$.

La función Takagi del parámetro ${\displaystyle w}$ es continua.^[3]​ De hecho, las funciones ${\displaystyle T_{w,n}}$ definidas por las sumas parciales ${\displaystyle T_{w,n}(x)=\sum _{k=0}^{n}w^{k}s(2^{k}x)}$ son continuas y converge uniformemente hacia ${\displaystyle T_{w}}$, ya que:

${\displaystyle \left|T_{w}(x)-T_{w,n}(x)\right|=\left|\sum _{k=n+1}^{\infty }w^{k}s(2^{k}x)\right|=\left|w^{n+1}\sum _{k=0}^{\infty }w^{k}s(2^{k+n+1}x)\right|\leq {\frac {|w|^{n+1}}{2}}\cdot {\frac {1}{1-|w|}}}$ para todo x cuando ${\displaystyle |w|<1}$.

Este valor se puede hacer tan pequeño como se quiera seleccionando un valor suficientemente grande de n. Por lo tanto, según el teorema del límite uniforme, ${\displaystyle T_{w}}$ es continua si |w| <1.

• 
  Parámetro w=2/3
• 
  Parámetro w=1/2
• 
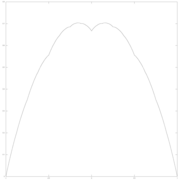  Parámetro w=1/3
• 
  Parámetro w=1/4
• 
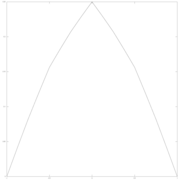  Parámetro w=1/8

Subaditividad

Dado que el valor absoluto es una función subaditiva, también lo es la función ${\displaystyle s(x)=\min _{n\in {\mathbf {Z} }}|x-n|}$ y sus dilataciones ${\displaystyle s(2^{k}x)}$. Dado que las combinaciones lineales positivas y los límites puntuales de las funciones subaditivas son subaditivas, la función de Takagi es subaditiva para cualquier valor del parámetro ${\displaystyle w}$.

El caso especial de la parábola

Para ${\displaystyle w=1/4}$, se obtiene una parábola. De hecho, la construcción de la parábola por subdivisión del punto medio ya fue descrita por Arquímedes.^[1]​

Diferenciabilidad

Para los valores del parámetro ${\displaystyle 0<w<1/2}$, la función de Takagi ${\displaystyle T_{w}}$ es diferenciable en sentido clásico en cualquier ${\displaystyle x\in \mathbb {R} }$ que no sea un número racional diádico.^[4]​ Precisamente, por derivación bajo el signo de la serie, para cualquier ${\displaystyle x\in \mathbb {R} }$ racional no diádico que se desee

${\displaystyle T_{w}'(x)=\sum _{n=0}^{\infty }(2w)^{n}\,(-1)^{x_{-n-1}}}$

donde ${\displaystyle (x_{n})_{n\in \mathbb {Z} }\in \{0,1\}^{\mathbb {Z} }}$ es la secuencia de dígitos en la expresión binaria de ${\displaystyle x}$, es decir, ${\displaystyle x=\sum _{n\in \mathbb {Z} }2^{n}x_{n}}$. Además, para estos valores de ${\displaystyle w}$, la función ${\displaystyle T_{w}}$ es lipschitziana de constante ${\displaystyle 1 \over 1-2w}$. En particular para el valor especial ${\displaystyle w=1/4}$, se tiene que para cualquier ${\displaystyle x\in [0,1]}$ racional no diádico ${\displaystyle T_{1/4}'(x)=2-4x}$, de acuerdo con el mencionado ${\displaystyle T_{1/4}(x)=2x(1-x).}$

Para ${\displaystyle w=1/2}$, la función del manjar blanco ${\displaystyle T_{w}}$ es de variación acotada en cualquier conjunto abierto no vacío; ni siquiera es lipschitziana localmente, pero es casi-lipschitziana. De hecho, admite la función ${\displaystyle \omega (t):=t(|\log _{2}t|+1/2)}$ como módulo de continuidad.^[5]​

Expansión en series de Fourier

La función Takagi-Landsberg admite una expansión en series de Fourier absolutamente convergente:

${\displaystyle T_{w}(x)=\sum _{m=0}^{\infty }a_{m}\cos(2\pi mx)}$

con ${\displaystyle a_{0}=1/4(1-w)}$ y, para ${\displaystyle m\geq 1}$

${\displaystyle a_{m}:=-{\frac {2}{\pi ^{2}m^{2}}}(4w)^{\nu (m)},}$

donde ${\displaystyle 2^{\nu (m)}}$ es la potencia máxima de ${\displaystyle 2}$ que divide a ${\displaystyle m}$. De hecho, la onda triangular ${\displaystyle s(x)}$ anterior posee una expansión en series de Fourier absolutamente convergente

${\displaystyle s(x)={\frac {1}{4}}-{\frac {2}{\pi ^{2}}}\sum _{k=0}^{\infty }{\frac {1}{(2k+1)^{2}}}\cos {\big (}2\pi (2k+1)x{\big )}.}$

Por convergencia absoluta, se puede reordenar la serie doble correspondiente para ${\displaystyle T_{w}(x)}$:

${\displaystyle T_{w}(x):=\sum _{n=0}^{\infty }w^{n}s(2^{n}x)={\frac {1}{4}}\sum _{n=0}^{\infty }w^{n}-{\frac {2}{\pi ^{2}}}\sum _{n=0}^{\infty }\sum _{k=0}^{\infty }{\frac {w^{n}}{(2k+1)^{2}}}\cos {\big (}2\pi 2^{n}(2k+1)x{\big )}\,:}$

poniendo ${\displaystyle m=2^{n}(2k+1)}$ se genera la serie de Fourier anterior para ${\displaystyle T_{w}(x).}$

Auto semejanza

La definición recursiva permite dar el monoide de auto-simetrías de la curva. Este monoide viene dado por dos generadores, g y r, que actúan en la curva (restringida al intervalo unitario) como

${\displaystyle [g\cdot T_{w}](x)=T_{w}\left({\frac {x}{2}}\right)={\frac {x}{2}}+wT_{w}(x)}$

y

${\displaystyle [r\cdot T_{w}](x)=T_{w}(1-x)=T_{w}(x)}$.

Un elemento general del monoide tiene entonces la forma ${\displaystyle \gamma =g^{a_{1}}rg^{a_{2}}r\cdots rg^{a_{n}}}$ para algunos enteros ${\displaystyle a_{1},a_{2},\cdots ,a_{n}}$ que actúa en la curva como una función lineal: ${\displaystyle \gamma \cdot T_{w}=a+bx+cT_{w}}$ para algunas constantes a, b y c. Debido a que la acción es lineal, se puede describir en términos de un espacio vectorial, con la base:

${\displaystyle 1\mapsto e_{1}={\begin{bmatrix}1\\0\\0\end{bmatrix}}}$

${\displaystyle x\mapsto e_{2}={\begin{bmatrix}0\\1\\0\end{bmatrix}}}$

${\displaystyle T_{w}\mapsto e_{3}={\begin{bmatrix}0\\0\\1\end{bmatrix}}}$

En este representación, la acción de g y r viene dada por

${\displaystyle g={\begin{bmatrix}1&0&0\\0&{\frac {1}{2}}&{\frac {1}{2}}\\0&0&w\end{bmatrix}}}$

y

${\displaystyle r={\begin{bmatrix}1&1&0\\0&-1&0\\0&0&1\end{bmatrix}}}$

Es decir, la acción de un elemento general ${\displaystyle \gamma }$ aplica la curva del manjar blanco en el intervalo unitario [0,1] a un subintervalo ${\displaystyle [m/2^{p},n/2^{p}]}$ para algunos enteros m, n, p. la aplicación viene dado exactamente por ${\displaystyle [\gamma \cdot T_{w}](x)=a+bx+cT_{w}(x)}$ donde los valores de a, b y c se puede obtener directamente multiplicando las matrices anteriores. Es decir:

${\displaystyle \gamma ={\begin{bmatrix}1&{\frac {m}{2^{p}}}&a\\0&{\frac {n-m}{2^{p}}}&b\\0&0&c\end{bmatrix}}}$

Téngase en cuenta que obtener ${\displaystyle p=a_{1}+a_{2}+\cdots +a_{n}}$ es inmediato.

El monoide generado por g y r a veces se denomina monoide diádico, un sub-monoide del grupo modular. Cuando se habla del grupo modular, la notación más común para g y r es T y S, pero esa notación entra en conflicto con los símbolos utilizados aquí.

La representación tridimensional anterior es solo una de las muchas representaciones que puede tener; muestra que la curva del manjar blanco es una posible realización de la acción. Es decir, hay representaciones para cualquier dimensión, no solo para 3, de forma que algunas de ellas generan la curva de De Rham.

Integración de la curva del manjar blanco

Dado que la integral de ${\displaystyle {\rm {blanc}}(x)}$ de 0 a 1 es 1/2, la identidad ${\displaystyle {\rm {blanc}}(x)={\rm {blanc}}(2x)/2+s(x)}$ permite que la integral sobre cualquier intervalo sea calculada por la siguiente relación recursiva, con el tiempo de cálculo en el orden del logaritmo de la precisión requerida. Definiendo

${\displaystyle I(x)=\int _{0}^{x}{\rm {blanc}}(y)\,dy}$

se tiene que

${\displaystyle I(x)={\begin{cases}I(2x)/4+x^{2}/2&{\text{if }}0\leq x\leq 1/2\\1/2-I(1-x)&{\text{if }}1/2\leq x\leq 1\\n/2+I(x-n)&{\text{if }}n\leq x\leq (n+1)\\\end{cases}}}$

La integral viene dado por:

${\displaystyle \int _{a}^{b}{\rm {blanc}}(y)\,dy=I(b)-I(a).}$

Se puede obtener una expresión más general definiendo

${\displaystyle S(x)=\int _{0}^{x}s(y)dy={\begin{cases}x^{2}/2,&0\leq x\leq {\frac {1}{2}}\\-x^{2}/2+x-1/4,&{\frac {1}{2}}\leq x\leq 1\\n/4+S(x-n),&(n\leq x\leq n+1)\end{cases}}}$

lo que combinado con la representación en serie da

${\displaystyle I_{w}(x)=\int _{0}^{x}T_{w}(y)dy=\sum _{n=0}^{\infty }(w/2)^{n}S(2^{n}x)}$

teniendo en cuenta que

${\displaystyle I_{w}(1)={\frac {1}{4(1-w)}}}$

Esta integral también es auto-semejante en el intervalo unitario, bajo una acción del monoide diádico descrito en la sección Autosemejanza. Aquí, la representación es de 4 dimensiones y tiene la base ${\displaystyle \{1,x,x^{2},I(x)\}}$. Reescribiendo lo anterior en el intervalo unitario para que la acción de g sea más clara, se tiene que

${\displaystyle [g\cdot I_{w}](x)=I_{w}\left({\frac {x}{2}}\right)={\frac {x^{2}}{8}}+{\frac {w}{2}}I_{w}(x)}$.

A partir de esto, se pueden obtener inmediatamente los generadores de la representación en cuatro dimensiones:

${\displaystyle g={\begin{bmatrix}1&0&0&0\\0&{\frac {1}{2}}&0&0\\0&0&{\frac {1}{4}}&{\frac {1}{8}}\\0&0&0&{\frac {w}{2}}\end{bmatrix}}}$

y

${\displaystyle r={\begin{bmatrix}1&1&1&{\frac {1}{4(1-w)}}\\0&-1&-2&0\\0&0&1&0\\0&0&0&-1\end{bmatrix}}}$

Las integrales repetidas se transforman bajo una representación de 5,6, ... dimensiones.

Relación con los complejos simpliciales

Sea

${\displaystyle N={\binom {n_{t}}{t}}+{\binom {n_{t-1}}{t-1}}+\ldots +{\binom {n_{j}}{j}},\quad n_{t}>n_{t-1}>\ldots >n_{j}\geq j\geq 1.}$

Definiendo la función de Kruskal-Katona

${\displaystyle \kappa _{t}(N)={n_{t} \choose t+1}+{n_{t-1} \choose t}+\dots +{n_{j} \choose j+1}.}$

el teorema de Kruskal-Katona establece que este es el número mínimo de (t − 1)-simplex que son caras de un conjunto de N t-simplex.

A medida que t y N se acercan al infinito, ${\displaystyle \kappa _{t}(N)-N}$ (adecuadamente normalizada) se aproxima a la curva del manjar blanco.

Véase también

• Función de Cantor (también conocida como la escalera del diablo)
• Función signo de interrogación de Minkowski
• Función de Weierstrass
• Transformación diádica

Referencias

Bibliografía

• Weisstein, Eric W. «Blancmange Function». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Takagi, Teiji (1901), «A Simple Example of the Continuous Function without Derivative», Proc. Phys.-Math. Soc. Jpn. 1: 176-177, doi:10.11429/subutsuhokoku1901.1.F176 .
• Benoît Mandelbrot, "Paisajes fractales sin pliegues y con ríos", que aparece en La ciencia de las imágenes fractales , ed. Heinz-Otto Peitgen, Dietmar Saupe; Springer-Verlag (1988) págs. 243 y 260.
• Linas Vepstas, Symmetries of Period-Doubling Maps , (2004)
• Donald Knuth, The Art of Computer Programming, volumen 4a. Algoritmos combinatorios, parte 1. ISBN 0-201-03804-8. Consúltense las páginas 372–375.

Lecturas relacionadas

• Allaart, Pieter C.; Kawamura, Kiko (11 de octubre de 2011), The Takagi function: a survey, Bibcode:2011arXiv1110.1691A, arXiv:1110.1691 .
• Lagarias, Jeffrey C. (17 de diciembre de 2011), The Takagi Function and Its Properties, Bibcode:2011arXiv1112.4205L, arXiv:1112.4205 .

Enlaces externos

• Takagi Explorer
• (Algunas propiedades de la función Takagi)