Triakistetraeder

Polyeder Triakistetraeder
3D-Ansicht eines Triakistetraeders (Animation)
Anzahl der Seitenflächen	12
Art der Seitenflächen	12 gleich­schenk­lige Dreiecke
Anzahl Ecken	8
Art der Ecken	4 × {3.3.3.3.3.3} + 4 × {3.3.3}
Anzahl Kanten	18
Schläfli-Symbol
dual zu	Tetraederstumpf
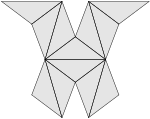Körpernetz eines Triakistetraeders

Das Triakistetraeder ist ein konvexes Polyeder, das sich aus 12 gleichschenkligen Dreiecken zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum Tetraederstumpf und hat 8 Ecken sowie 18 Kanten.

Werden auf alle 4 Begrenzungsflächen eines Tetraeders (mit Kantenlänge ${\displaystyle a}$) Pyramiden mit der Flankenlänge ${\displaystyle b}$ aufgesetzt, entsteht ein Triakistetraeder, sofern die Bedingung ${\displaystyle {\tfrac {a}{3}}{\sqrt {3}}<b<{\tfrac {a}{2}}{\sqrt {2}}}$ erfüllt ist.

• Für den zuvor genannten minimalen Wert von ${\displaystyle b}$ haben die aufgesetzten Pyramiden die Höhe 0, sodass lediglich das Tetraeder mit der Kantenlänge ${\displaystyle a}$ übrig bleibt.
• Das spezielle Triakistetraeder mit gleichen Flächenwinkeln entsteht, wenn ${\displaystyle b={\tfrac {3}{5}}a}$ ist.
• Nimmt ${\displaystyle b}$ den o. g. maximalen Wert an, entartet das Triakistetraeder zu einem Würfel mit der Kantenlänge ${\displaystyle b}$ (siehe Grafik links); dieser vierfach geschnittene Würfel – mit einem gedachten Tetraeder im Kern – ist topologisch gleichwertig zum Triakistetraeder.
• Überschreitet ${\displaystyle b}$ den maximalen Wert, so ist das Polyeder nicht mehr konvex und entartet zu einem Sternkörper.

Allgemein ${\displaystyle {\tfrac {a}{3}}{\sqrt {3}}<b<{\tfrac {a}{2}}{\sqrt {2}}}$ Größen eines Triakistetraeders mit Kantenlängen a, b Volumen ${\displaystyle V={\frac {a^{2}}{12}}\left(a{\sqrt {2}}+4{\sqrt {3b^{2}-a^{2}}}\right)}$ Oberflächeninhalt ${\displaystyle A_{O}=3a{\sqrt {4b^{2}-a^{2}}}}$ Pyramidenhöhe ${\displaystyle k={\frac {1}{3}}{\sqrt {9b^{2}-3a^{2}}}}$ Inkugelradius ${\displaystyle \rho ={\frac {a}{12}}{\sqrt {\frac {48b^{2}-14a^{2}+8a{\sqrt {6b^{2}-2a^{2}}}}{4b^{2}-a^{2}}}}}$ Flächenwinkel  (über Kante a) ${\displaystyle \cos \,\alpha _{1}={\frac {5a^{2}-12b^{2}-8a{\sqrt {6b^{2}-2a^{2}}}}{9(4b^{2}-a^{2})}}}$ Flächenwinkel  (über Kante b) ${\displaystyle \cos \,\alpha _{2}={\frac {2b^{2}-a^{2}}{4b^{2}-a^{2}}}}$

Speziell ${\displaystyle b={\tfrac {3}{5}}a}$ Größen eines Triakistetraeders mit Kantenlänge a Volumen ${\displaystyle V={\frac {3}{20}}\,a^{3}{\sqrt {2}}}$ Oberflächeninhalt ${\displaystyle A_{O}={\frac {3}{5}}\,a^{2}{\sqrt {11}}}$ Pyramidenhöhe ${\displaystyle k={\frac {a}{15}}{\sqrt {6}}}$ Inkugelradius ${\displaystyle \rho ={\frac {3}{4}}\,a\,{\sqrt {\frac {2}{11}}}}$ Kantenkugelradius ${\displaystyle r={\frac {a}{4}}{\sqrt {2}}}$ Flächenwinkel  ≈ 129° 31′ 16″ ${\displaystyle \cos \,\alpha =-{\frac {7}{11}}}$ Sphärizität  ≈ 0,86439 ${\displaystyle \Psi ={\frac {\sqrt[{3}]{60\,\pi }}{2{\sqrt {11}}}}}$

Commons: Triakistetraeder – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Triakistetraeder – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• Eric W. Weisstein: Triakistetraeder. In: MathWorld (englisch).
• Mineralienatlas:Triakistetraeder Interaktive Darstellung des Triakistetraeders im Mineralienatlas